Cẩm nang luyện thi đại học môn vật lý ( hay, chuẩn)

CHƯƠNG I. DAO ĐỘNG CƠ

Bài 1. ĐẠI CƯƠNG VỀ DAO ĐỘNG ĐIỀU HÒA

Dạng 1: Nhận biết phương trình dao động.

Phương pháp 

a. Xác định \(A,\varphi ,\omega ...\)

- Đưa các phương trình về dạng chuẩn nhờ cá công thức lượng giác

- So sánh với phương trình chuẩn để suy ra: \(A,\varphi ,\omega ...\)

b. Suy ra cách kích thích dao động:

Thay t = 0 vào phương trình \(\left\{\begin{matrix}x=Acos(\omega t+\varphi ) \\ v=-A\omega sin(\omega t+\varphi ) \end{matrix}\right.\Rightarrow \left\{\begin{matrix}x_{0}=? \\ v_{0}=? \end{matrix}\right.\Rightarrow\) Cách kích thích dao động

c. Chú ý:

- Phương trình chuẩn: \(x=Acos(\omega t+\varphi );v=-\omega Asin(\omega t+\varphi ),a=-\omega ^{2}Acos(\omega t+\varphi )\)

- Một số công thức lượng giác:

\(x=Asin(\omega t+\varphi )=Acos(\omega t+\varphi-\frac{\pi }{2} );x=Acos(\varphi -\omega t )=Acos(\omega t-\varphi )\)

\(x=Asin(\omega t+\varphi )=Acos(\omega t+\varphi-\frac{\pi }{2} );x-=Acos(\omega t+\varphi )\) \(=Acos(\omega t+\varphi+\pi )\)

- Công thức: \(\omega =\frac{2\pi }{T}=2\pi f\Rightarrow \left\{\begin{matrix}T=\frac{2\pi }{\omega } \\ f=\frac{\omega }{2\pi } \end{matrix}\right.\)

- Chu kì và tần số tính theo số dao động N thực hiện được trong thời gian \(\Delta t:T=\frac{\Delta t}{N},f=\frac{N}{\Delta t}\)

Dạng 2: Xác định li độ, vận tốc và gia tốc tại thời điểm t biết trước.

Phương pháp:

- Muốn xác định x, v, a ở thời điêm hay ứng với pha đã cho ta chỉ cân thay t hay pha đã cho vào công thức:  

\(x=Acos(\omega t+\varphi );v=-\omega Asin(\omega t+\varphi ),a=-\omega ^{2}Acos(\omega t+\varphi )\)

- Nếu đã xác định được li độ x, ta có thể xác định gia tốc biểu thức như sau: \(a=-\omega ^{2}x\)

- Chú ý: 

+ khi \(v> 0,a> 0\): Vận tốc, gia tốc, lực phục hồi cùng chiều với chiều dương tọa độ

+ Khi \(v< 0,a< 0\): Vận tốc, gia tốc, lực phục hồi ngược chiều với chiều dương tọa độ

+ Để xác định tính chất chuyển động ở một thời điểm ta phải căn cứ vào li độ và chiều của vận tốc cuả vật ở thời điểm đó để kết luận theo sơ đồ sau:

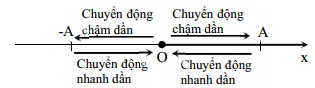
Dạng 3: Vận tốc và gia tốc cực đại

Phương pháp:

1. Vận tốc trong dao động điều hòa: \(v=x^{'}=-A\omega sin(\omega t+\varphi )=\omega Acos(\omega t+\varphi+\frac{\pi }{2} )\)

+ \(\begin{vmatrix} v_{max} \end{vmatrix}=\omega A\Leftrightarrow x=0\) (tại VTCB)

+ \(v_{min}=0\Leftrightarrow x=\pm A\) (tại hai biện)

2. Gia tốc trong dao động điều hòa : \(a=v^{'}=x^{''}=-A\omega _{2}cos(\omega t+\varphi )=-\omega ^{2}x\)

+ \(\begin{vmatrix} a_{max} \end{vmatrix}=\omega^{2} A\Leftrightarrow x=\pm A\) (tại VTCB)

+ \(a_{min}=0\Leftrightarrow x=0\) (tại hai biện)

+ \(\overrightarrow{a}\) luôn hướng về VTCB. A luôn ngược dấu với x

+ Hệ quả: \(\frac{a_{max}}{v_{max}}=\omega =2\pi f=\frac{2\pi }{T}\)

-----------------------------------------------Các chương khác bạn đọc tải tài liệu sẽ thấy nha---------------------------

CHƯƠNG VII. HẠT NHÂN NGUYÊN TỬ 

Bài 1. CẤU TẠO HẠT NHÂN

Dạng 1: Hệ thức anhxtanh

Phương pháp

- Áp dụng công thức:

+ Khối lượng tương đối:  \(m=\frac{m_{0}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\)

+ Năng lượng toàn phần: \(E=mc^{2}=\frac{m_{0}c^{2}}{\sqrt{1-\frac{v^{2}}{c^{2}}}}\) 

+ Năng lượng nghỉ: \(E_{0}=m_{0}c^{2}\)

+ Năng lượng tuowng đối cuả vật: \(K=E-E_{0} =(m-m_{0})c^{2}=m_{0}c^{2}\left ( \frac{1}{1-\sqrt{\frac{v^{2}}{c^{2}}}} -1\right )\)

+ Định lí về biến thiên động năng: \(K_{2}-K_{1}=\sum A\)

+ Công thức của lực điện trường tác dụng lên một điện tích: A = qEd

Dạng 2: Xác định cấu tạo hạt nhân

Phương pháp:

- Áp dụng công thức: Hạt nhân \(_{Z}^{A}\textrm{X}\) có: A nuclon, Z proton, (A-Z) notron

Dạng 3: Tính bán kính, thể tích, khối lượng riêng của hạt nhân. Tính số hạt, tỉ lệ phần trăm đồng vị

Phương pháp:

- Bán kính hạt nhân: \(R=1,2.10^{-15}.a^{\frac{1}{3}}(m)\)

- Thể tích hạt nhân: \(V=\frac{4\pi }{3}R^{3}\)

- Khối lượng riêng hạt nhân: \(p=\frac{m_{hatnhan}}{V}\)

- Số hạt trong m gam chất đơn nguyên tử: \(N=\frac{m}{A}N_{A}\) với \(N_{A}=6,02.10^{23}mol^{-1}\)

Dạng 4: Tính hụt khối, năng lượng liên kết và năng lượng liên kết riêng.

Phương pháp:

- Độ hụt khối của hạt nhân \(_{Z}^{A}\textrm{X}\): \(\Delta m= Zm_{p}+(A-Z)m_{n}-m_{X}\)

- Đơn vị khối lượng nguyên tử: \(1u=1,66055.10^{-27}kg=931,5\frac{MeV}{c^{2}}\)

- Năng lượng liên kết của hạt nhân \(_{Z}^{A}\textrm{X}\): \(\left\{\begin{matrix}W_{lk}=\Delta mc^{2}=\begin{bmatrix} Zm_{p}+(A-Z)m_{n}-m_{X} \end{bmatrix}c^{2} \\ W_{lk}=\begin{bmatrix} Zm_{p}+(A-Z)m_{n}-m_{X} \end{bmatrix}.931,5(MeV) \end{matrix}\right.\)

- Năng lượng liên kết riêng: \(\varepsilon =\frac{W_{lk}}{A}\)

- Hạt nhân có năng lượng liên kết càng lớn thì càng bền vững. Những hạt nhân bền có số khối nằm trong khoảng từ 50 đến 95, hạt nhân bền nhất có \(\varepsilon =8,8\frac{MeV}{nuclon}\)