Giao thoa với nguồn ánh sáng đơn sắc ( hay, đầy đủ)

GIAO THOA VỚI NGUỒN ÁNH SÁNG ĐƠN SẮC

I. Lý thuyết

1. Khái niện về giao thoa ánh sáng.

a. Hiện tượng giao thoa ánh sáng

   -Hai chùm sáng kết hợp là hai chùm phát ra ánh sáng có cùng tần số và cùng pha hoặc có độ lệch pha không đổi theo thời gian.

   -Khi hai chùm sáng kết hợp gặp nhau chúng sẽ giao thoa:

      +Những chổ hai sóng gặp nhau mà cùng pha nhau, chúng tăng cường lẫn nhau tạo thành các vân sáng.

      +Những chổ hai sóng gặp nhau mà ngược pha với nhau, chúng triệt tiêu nhau tạo thành các vân tối.

   -Nếu ánh sáng trắng giao thoa thì hệ thống vân của các ánh sáng đơn sắc khác nhau sẽ không trùng nhau:

      +Ở chính giữa, vân sáng của các ánh sáng đơn sắc khác nhau nằm trùng nhau cho một vân sáng trắng gọi là vân trắng chính giữa ( vân trung tâm) .

      +Ở hai bên vân trung tâm, các vân sáng khác của các sóng ánh sáng đơn sắc khác nhau không trùng với nhau nữa, chúng nằm kề sát bên nhau và cho những quang phổ có màu như ở màu cầu vồng.

   -Hiện tượng giao thoa ánh sáng là bằng chứng thực nghiệm khẵng định ánh sáng có tính chất sóng. 

b.Vị trí vân, khoảng vân trong giao thoa ánh sáng khe Young

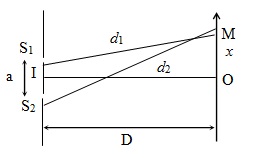
   + Vị trí vân sáng: x_s = k \(\frac{\lambda D}{a}\);  với k ∈ Z.

   + Vị trí vân tối:    x_t = (2k + 1)\(\frac{\lambda D}{2a}\) ; với k ∈ Z.

   + Khoảng vân :    i =\(\frac{\lambda D}{a}\) .   =>  Bước sóng: \(\lambda =\frac{ia}{D}\)

   + Giữa n vân sáng liên tiếp có (n – 1) khoảng vân.

   => Vị trí vân sáng: x_s = ki       

   =>  Vị trí vân tối:   x_t = (2k + 1)i/2    

c. Thí nghiệm Young có bản mặt song song :

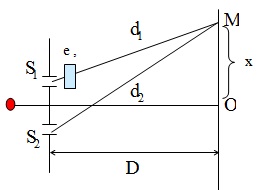
- Do có bản mỏng có bề dày là e, chiết suất n :

    + Quang lộ từ S₁ đến M là : S₁M = (d₁ – e)+ n.e

    + Quang lộ từ S₂ đến M là : S₂M = d₂

- Hiệu quang trình : δ = S₂M – S₁M = d₂ – d₁ – e (n-1) = \(\frac{ax}{D}\)  - e (n-1)

- Vị trí vân sáng :    x_s = k\(\frac{\lambda D}{a}\) + \(\frac{e.D}{a}\)(n-1)

- Vị trí vân tối :       x_t = (k + 0,5)\(\frac{\lambda D}{a}\) + \(\frac{e.D}{a}\)(n-1)

- Hệ vân dời một đoạn về phía có đặt bản mặt song song: x₀ = \(\frac{e.D}{a}\)(n-1)

d. Bước sóng và màu sắc ánh sáng

+ Ánh sáng đơn sắc là ánh sáng có một bước sóng xác định trong chân không.

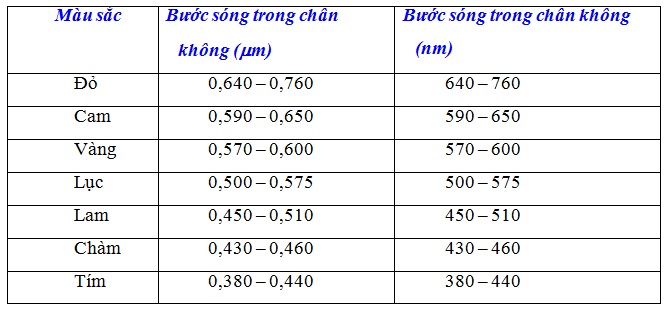
+ Mọi ánh sáng đơn sắc mà ta nhìn thấy (ánh sáng khả kiến) đều có bước sóng trong chân không (hoặc không khí) trong khoảng từ 0,38μm (ánh sáng tím) đến 0,76μm (ánh sáng đỏ).

+ Những màu chính trong quang phổ ánh sáng trắng (đỏ, cam, vàng, lục, lam, chàm, tím) ứng với từng vùng có bước sóng lân cận nhau. Bảng màu và bước sóng của ánh sáng trong chân không như sau:

2. Giao thoa khe Young với ánh sáng đơn sắc.

a. Các công thức:

- Hiệu quang trình : δ = S₂M – S₁M = \(n\frac{ax}{D}\)

+ Vị trí vân sáng: x_s = k \(\frac{\lambda D}{a}\);  với k ∈ Z.

+ Vị trí vân tối:   + Vị trí vân tối:  x_t = (2k + 1)\(\frac{\lambda D}{2a}\) ; với k ∈ Z.
 Hay  x_t = (k + 0,5) \(\frac{\lambda D}{a}\)

 + Khoảng vân :  i =\(\frac{\lambda D}{a}\)

+ Giữa n vân sáng(hoặc vân tối) liên tiếp có (n – 1) khoảng vân.

 +  Bước sóng: \(\lambda =\frac{ia}{D}\)

b.Giao thoa trong môi trường chiết suất n :

   - Vị trí vân sáng : x_s = k\(\frac{\lambda _{0}D}{a.n}\)

   - Vị trí vân tối : x_t = (k + 0,5)\(\frac{\lambda _{0}D}{a.n}\)

   - Khoảng vân : i = \(\frac{\lambda _{0}D}{a.n}=\frac{i_{0}}{n}\)

Với \(\lambda _{0},i_{0}=\frac{\lambda _{0}D}{a}\): Bước sóng và khoảng vân  khi tiến hành thí nghiệm giao thoa trong không khí (n=1). 

c. Phương pháp giải:

+Để xác định vị trí vân sáng vân tối:

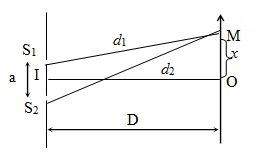
   Vị trí vân sáng: x_s = k\(\frac{\lambda D}{a}\); với k ∈ Z.

    Vị trí vân tối:   x_t = (2k + 1)\(\frac{\lambda D}{2a}\) ; với k ∈ Z.

                 Hay:    x_t = (k + 0,5)\(\frac{\lambda D}{a}\)         

+ Để xác định xem tại điểm M  trên vùng giao thoa có vân sáng (bậc mấy) hay vân tối ta  lập tỉ số: \(\frac{x_{M}}{i}=\frac{\overline{OM}}{i}\)

 để kết luận:      

   -Tại M có vân sáng khi:  \(\frac{x_{M}}{i}=\frac{\overline{OM}}{i}\) = k, đó là vân sáng bậc k.

   -Tại M có vân tối khi: \(\frac{x_{M}}{i}\) = (2k + 1) \(\frac{1}{2}\).

d. Các dạng bài tập Giao thoa với ánh sáng đơn sắc:

Dạng 1: Vị trí vân sáng- vị trí vân tối- khoảng vân:

a-      Khoảng vân: là khoảng cách giữa 2 vân sáng liền kề :

 i = \(\frac{\lambda D}{a}\)    ( i phụ thuộc λ )

=> khoảng vân của các ánh sáng đơn sắc khác  nhau là khác nhau với cùng một thí nghiệm.

   b- Vị trí vân sáng bậc k: Tại đó ứng với ∆d = d₂ – d₁ = k.λ, đồng thời 2 sóng ánh sáng truyền tới cùng pha:  

   \(x_{s}^{k}=\pm k.\frac{\lambda .D}{a}=\pm k.i\)

                   k = 0: ứng với vân sáng trung tâm (hay ∆d = 0)

                   k = ± 1: ứng với vân sáng bậc 1

                   …………

                   k =± n: ứng với vân sáng bậc n.

c- Vị trí vân tối thứ k + 1: Tại đó ứng với d =(k + \(\frac{1}{2}\) ).λ . Là vị trí hai sóng ánh sáng truyền tới ngược pha nhau.:

    \(x_{T}^{k+1}=\pm (k+\frac{1}{2}).\frac{\lambda D}{a}=\pm (k+\frac{1}{2})i\) . Hay vân tối thứ k: \(x_{T}^{k}\) = (k - 0,5).i.

Ví dụ: Vị trí vân sáng bậc 5 là: \(x_{s}^{5}\) = 5.i   Vị trí vân tối thứ 4: \(x_{T}^{4}\) = 3,5.i (Số thứ vân – 0,5).

Dạng 2: Khoảng cách giữa các vân

Loại 1- Khoảng cách vân cùng bản chất liên tiếp: l = (số vân – 1).i

Ví dụ 1: khoảng cách giữa 7 vân sáng liên tiếp: l = (7 – 1).i = 6i

Loại 2- Giữa một vân sáng và một vân tối bất kỳ:

Giả sử xét khoảng cách vân sáng bậc k và vân tối thứ k’, vị trí: \(x_{s}^{k}\) = k.i; \(x_{T}^{k}\)=(k – 0,5).i

Nếu:     + Hai vân cùng phía so với vân trung tâm: ∆x= | \(x_{s}^{k}\) - \(x_{t}^{k'}\) |

+Hai vân khác phía so với vân trung tâm:  ∆x= \(x_{s}^{k}\) + \(x_{t}^{k'}\) 

-Khoảng cách giữa vân sáng và vân tối liền kề là :  \(\frac{i}{2}\)

           => vị trí vân tối các thứ liên tiếp được xác định:

 \(x_{t}=k\frac{i}{2}\)  (với k lẻ: 1,3,5,7,….)

Ví dụ 2:  Tìm khoảng cách giữa vân sáng bậc 5 và vân tối thứ 6

Giải:  Ta có \(x_{s}^{5}=5i;x_{t}^{6}=(6-0,5)=5,5i\)

        + Nếu hai vân cùng phía so với vân trung tâm: \(\Delta x=x_{t}^{6}-x_{s}^{5}=5,5i-5i=0,5i\)

      + Nếu hai vân khac phía so với vân trung tâm :     \(\Delta x=x_{t}^{6}+ x_{s}^{5}=10,5i\)

Loại 3- Xác định vị trí điểm M  trên trường giao thoa cách vân trung tâm một khoảng x_M có vân sáng hay vân tối, bậc mấy ?

        + Lập tỉ số: \(\frac{x_{M}}{i}=n\) ;  Nếu n nguyên, hay n ∈ Z, thì tại M có vân sáng bậc k=n.

 Nếu n bán nguyên hay n=k+0,5 với k ∈ Z, thì tại M có vân tối thứ k +1

Dạng 3:  Xác định số vân trên trường giao thoa:

Cách 1:- Trường giao thoa xét là chiều rộng của khu vực chứa toàn bộ hiện tượng giao thoa hứng được trên màn- kí kiệu L.

- Số vân trên trường giao thoa:

          + Số vân sáng: N_s = 1+2.\(\left [ \frac{L}{2i} \right ]\)  Chia lấy phần nguyên

          + Số vân tối:    N_T = 2. \(\left [ \frac{L}{2i} +0,5 \right ]\)

- Số vân sáng, vân tối trong đoạn MN, với 2 điểm M, N thuộc trường giao thoa nằm 2 bên vân sáng trung tâm:

            + Số vân sáng: N_s =  \(\left [ \frac{OM}{i} \right ]+\left [ \frac{ON}{i} \right ]\) +1.

            + Số vân tối:     N_T = \(\left [ \frac{OM}{i} +0,5 \right ]+\left [ \frac{ON}{i}+0,5 \right ]\)

- Số vân sáng, tối giữa 2 điểm MN trong đoạn giao thoa nằm cùng phía so với vân sáng trung tâm:

            + Số vân sáng: N_s = \(\left [ \frac{OM}{i} \right ]-\left [ \frac{ON}{i} \right ]\)

            + Số vân tối:     N_T = \(\left [ \frac{OM}{i} +0,5 \right ]-\left [ \frac{ON}{i}+0,5 \right ]\) .Với M, N không phải là vân sáng.

Cách 2:

+Để xác định số vân sáng - tối  trong miền giao thoa có bề rộng  L  ta tính số khoảng vân trên nửa trường giao thoa trường bằng cách chia nửa giao thoa trường cho i và ta có kết quả: \(\frac{L}{2i} =n+x\)    (phần lẻ)

Ta xác định số vân sáng trên giao thoa trường ta phải nhân cho 2 nên ta có:

+ Số vân sáng: 2n + 1: (1 : vân sáng trung tâm)

+ Số vân tối:        * Nếu x ≥  0.5: 2n + 2

* Nếu x < 0.5: 2n

VD 1: \(\frac{L}{2i}=8.5=8+0,5\) =>  Số vân sáng: 2.8 +1=17;  Số vân tối: 2.8 + 2=18

VD 2: \(\frac{L}{2i}=8.3=8+0,3\) =>  Số vân sáng: 2.8 +1=17; Số vân tối: 2.8 = 16

+Khoảng cách giữa hai vân: ∆X

- Cùng bên so với vân sáng TT: \(\Delta x=\left | x_{ion} \right |-\left | x_{nho} \right |\)

- Khác bên so với vân sáng TT:\(\Delta x=\left | x_{ion} \right |+\left | x_{nho} \right |\)

Ví dụ 4:  Trong một thí nghiệm về Giao thoa anhs sáng bằng khe I âng với ánh sáng đơn sắc  λ = 0,7 μm, khoảng cách giữa 2 khe s₁,s₂ là a = 0,35 mm, khoảng cách từ 2 khe đến màn quan sát là D = 1m, bề rộng của vùng có giao thoa là 13,5 mm. Số vân sáng, vân tối quan sát được trên màn là:

A: 7 vân sáng, 6 vân tối;                                      B: 6 vân sáng, 7 vân tối.

C: 6 vân sáng, 6 vân tối;                                      D: 7 vân sáng, 7 vân tối.

Giải:  Khoảng  vân  i =  \(\frac{\lambda D}{a}=\frac{0,7.10^{-6}.1}{0,35.10^{-3}}\) = 2.10^-3m = 2mm.;  Số vân sáng: N_s = 2.\(\left [ \frac{L}{2i} \right ]\)+1 = 2.[3,375] +1 = 7.

        Phần thập phân của \(\frac{L}{2i}\) là 0,375 < 0,5 nên số vạch tối là N_T = N_s – 1 = 6

Số vạch tối là 6, số vạch sáng là 7.

Các Bài tập:

Bài 1. Trong thí nghiệmYoung về giao thoa ánh sáng, hai khe S₁ và S₂ được chiếu bằng ánh sáng đơn sắc có bước sóng λ. Khoảng cách giữa hai khe là 0,8 mm, khoảng cách từ hai khe đến màn là 2 m. Người ta đo được khoảng cách giữa 6 vân sáng liên tiếp trên màn là 6 mm. Tính bước sóng của ánh sáng dùng trong thí nghiệm và khoảng cách từ vân sáng bậc 3 đến vân sáng bậc 8 ở cùng phía với nhau so với vân sáng chính giữa.

Giải  bài 1. Ta có: i = \(\frac{L}{6-1}\)= 1,2 mm; λ = \(\frac{ai}{D}\)= 0,48.10^-6 m; x₈ - x₃ = 8i – 3i = 5i = 6 mm.

Bài 2. Trong thí nghiệm Young về giao thoa ánh sáng, khoảng cách giữa hai khe là 1 mm, khoảng cách từ hai khe đến màn là 3 m. Dùng ánh sáng đơn sắc có bước sóng l chiếu vào hai khe thì người ta đo được khoảng cách từ vân sáng trung tâm tới vân sáng thứ tư là 6 mm. Xác định bước sóng l và vị trí vân sáng thứ 6.

Giải  bài 2. Ta có: i = \(\frac{L}{5-1}\)  = 1,5 mm; λ = \(\frac{ai}{D}\)= 0,5.10^-6 m; x₆ = 6i = 9 mm.

Bài 3. Trong thí nghiệm của Young về giao thoa ánh sáng, hai khe S₁ và S₂ được chiếu bằng ánh sáng đơn sắc có bước sóng λ = 0,4 μm. Khoảng cách giữa hai khe là 0,4 mm, khoảng cách từ hai khe đến màn là 2 m. Xác định khoảng cách giữa 9 vân sáng liên tiếp và khoảng cách từ vân sáng 4 đến vân sáng 8 ở khác phía nhau so với vân sáng chính giữa.

Giải  bài 3. Ta có: i = \(\frac{\lambda D}{a}\) = 2 mm; L = (9 – 1)i = 16 mm; x₈ + x₄ = 8i + 4i = 12i = 24 mm.

Bài 4. Trong thí nghiệm của Young về giao thoa ánh sáng, hai khe S₁ và S₂ được chiếu bằng ánh sáng đơn sắc có bước sóng λ = 0,5 μm. Khoảng cách giữa hai khe là 0,8 mm. Người ta đo được khoảng cách giữa 5 vân sáng liên tiếp trên màn là 4 mm. Tính khoảng cách từ hai khe đến màn và cho biết tại 2 điểm C và E trên màn, cùng phía với nhau so với vân sáng trung tâm và cách vân sáng trung tâm lần lượt là 2,5 mm và 15 mm là vân sáng hay vân tối? Từ C đến E có bao nhiêu vân sáng?

Giải  bài 4. Ta có: i = \(\frac{L}{5-1}\) = 1 mm; D = \(\frac{ai}{D}\) = 1,6 m; \(\frac{x_{c}}{i}\)= 2,5 nên tại C ta có vân tối; \(\frac{x_{E}}{i}\)= 15 nên tại N ta có vân sáng; từ C đến E có 13 vân sáng kể cả vân sáng bậc 15 tại E.

Bài 5. Trong thí nghiệm của Young về giao thoa ánh sáng, hai khe S₁ và S₂ được chiếu bằng ánh sáng đơn sắc có bước sóng λ. Khoảng cách giữa hai khe là  0,8 mm, khoảng cách từ hai khe đến màn là 2 m. Người ta đo được khoảng cách giữa 6 vân sáng liên tiếp trên màn là  6 mm. Xác định bước sóng của ánh sáng dùng trong thí nghiệm và cho biết tại 2 điểm M và N trên màn, khác phía nhau so với vân sáng trung tâm và cách vân sáng trung tâm lần lượt là 3 mm và 13,2 mm là vân sáng hay vân tối? Nếu là vân sáng thì đó là vân sáng bậc mấy? Trong khoảng cách từ M đến N có bao nhiêu vân sáng?

Giải  bài 5. Ta có: i = \(\frac{L}{6-1}\) = 1,2 mm; λ = \(\frac{ai}{D}\) = 0,48.10^-6 m; \(\frac{x_{M}}{i}\)= 2,5 nên tại M ta có vân tối; \(\frac{x_{N}}{i}\)= 11 nên tại N ta có vân sáng bậc 11. Trong khoảng từ M đến N có 13 vân sáng không kể vân sáng bậc 11 tại N.

đáp án A.