Các dạng bài toán về độ lệch pha
Cập nhật lúc: 16:05 21-06-2015 Mục tin: Vật lý lớp 12
Bài toán về độ lệch pha là một dạng bài tập khó yêu cầu bạn đọc phải nắm vững lý thuyết về cách mạch điện cơ bản cũng như các công thức lượng giác trong toán học.
Xem thêm:
CÁC DẠNG BÀI TOÁN VỀ ĐỘ LỆCH PHA
1.Phương pháp chung:
+ \(tan\varphi =\frac{Z_{L}-Z_{C}}{R}\)Hay \(tan\varphi =\frac{U_{L}-U_{C}}{U_{R}}\) Thường dùng công thức này vì có dấu của j,
+ \(cos\varphi =\frac{R}{Z}\) Hay \(cos\varphi =\frac{U_{R}}{U};cos\varphi =\frac{P}{UI}\)Lưu ý công thức này không cho biết dấu của j.
+ \(sin\varphi =\frac{Z_{L}-Z_{C}}{Z}; sin\varphi =\frac{U_{L}-U_{C}}{U}\)
+ Kết hợp với các công thức định luật ôm :\(I=\frac{U_{R}}{R}=\frac{U_{L}}{Z_{L}}=\frac{U_{C}}{Z_{C}}=\frac{U}{Z}=\frac{U_{MN}}{Z_{MN}}\)
+ Lưu ý: Xét đoạn mạch nào thì áp dụng công thức cho đoạn mạch đó.
+Độ lệch pha của hai đoạn mạch ở trên cùng một mạch điện:\(\varphi _{1}-\varphi _{2}=\pm \Delta \varphi\) ,khi đó:
-Nếu (hai điện áp đồng pha) thì \(\varphi _{1}=\varphi _{2}\Rightarrow tan\varphi _{1}=tan\varphi _{2}\)
Lúc này ta có thể cộng các biên độ điện áp thành phần: \(U=U_{1}+U_{2}\Rightarrow Z=Z_{1}+Z_{2}\)
-Nếu \(\Delta \varphi\pm \frac{\pi }{2}\) (hai điện áp vuông pha),ta dùng công thức: \(tan\varphi _{1}.tan\varphi _{2}=-1\)
-Nếu \(\Delta \varphi\) bất kì ta dùng công thức : \(\Delta \varphi =\frac{tan\varphi _{1}-tan\varphi _{2}}{1+tan\varphi _{1}.tan\varphi _{2}}\) hoặc dùng giản đồ véc tơ.
+Thay giá trị tương ứng của hai đoạn mạch đã biết vào \(tan\varphi _{1}\) và \(tan\varphi _{2}\)(Với : \(tan\varphi =\frac{Z_{L}-Z_{C}}{R}\) )
2.Xác định các đại lượng khi biết hai đoạn mạch có điện áp cùng pha, vuông pha.
a.Các ví dụ:
Ví dụ 1: Cho mạch điện xoay chiều như hình bên.
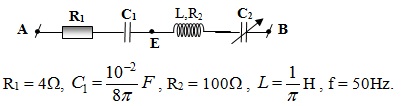
Tìm điện dung C2, biết rằng điện áp uAE và uEB đồng pha.
Bài giải: \(\varphi _{AE}=\varphi _{u_{AE}}-\varphi _{i};\varphi _{EB}=\varphi _{u_{EB}}-\varphi _{i}\) ;
Vì uAE và uEB đồng pha nên \(\varphi _{u_{AE}}=\varphi _{EB}\Rightarrow \varphi _{AE}=\varphi _{u_{EB}}\Rightarrow tan\varphi _{AE}=tan\varphi _{EB}\)
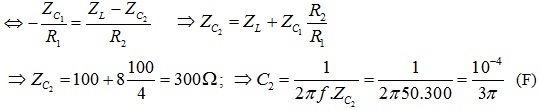
Ví dụ 2: Cho mạch điện như hình vẽ. UAN = 150V, UMB = 200V, uAN và uMB vuông pha với nhau, cường độ dòng điện tức thời trong mạch có biểu thức \(i=I_{0}cos100\pi t\) (A). Biết cuộn dây là thuần cảm. Hãy viết biểu thức uAB.
![]()
Bài giải:Ta có: \(U_{AN}=\sqrt{{U_{R}}^{2}+{U_{C}}^{2}}=150V(1);U_{MB}=\sqrt{{U_{R}}^{2}+{U_{L}}^{2}}=200V(2)\)
Vì uAN và uMB vuông pha nhau nên: \(\varphi _{MB}-\varphi _{AN}=\frac{\pi }{2}\Rightarrow \varphi _{MB}=\frac{\pi }{2}+\varphi _{AN}\) (Với \(\varphi _{MB}> 0,\varphi _{AN}< 0\) )
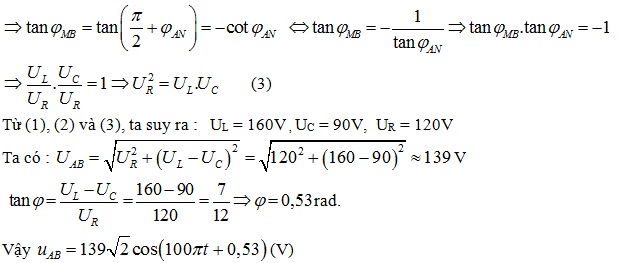
Ví dụ 3: Cho vào đoạn mạch hình bên một dòng điện xoay chiều có cường độ \(i=I_{0}cos100\pi t\)(A). Khi đó uMB và uAN vuông pha nhau, và \(u_{MB}=100\sqrt{2}cos(100\pi t+\frac{\pi }{3})\)(V). Hãy viết biểu thức uAN và tìm hệ số công suất của đoạn mạch MN.
![]()
Bài giải: Do pha ban đầu của i bằng 0 nên
\(\varphi _{MB}=\varphi _{u_{MB}}-\varphi _{i}=\frac{\pi }{3}-0=\frac{\pi }{3} rad\)
Dựa vào giản đồ vec-tơ, ta có các giá trị hiệu dụng của UL, UR, UC là:
UR = UMB cos φMB = \(100cos\frac{\pi }{3}=50(V)\)
\(U_{L} = U_{R} tan \varphi _{MB} = 50tan\frac{\pi }{3}=50\sqrt{3}(V)\)
Vì uMB và uAN vuông pha nhau nên:\(\varphi _{MB}-\varphi _{AN}=\frac{\pi }{2}\Rightarrow \varphi _{AN}=-\frac{\pi }{6}\)
Ta có:\(tan\varphi _{MB}.tan\varphi _{AN}=-1\) (V)
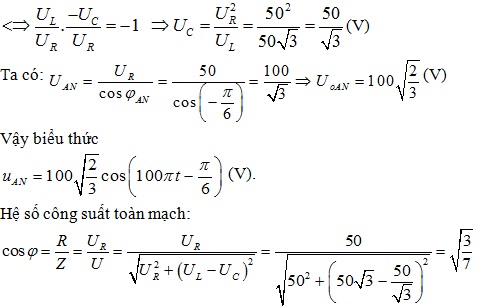
Ví dụ 4: Cho đoạn mạch xoay chiều u = U0cosωt ổn định , có R ,L , C ( L thuần cảm )mắc nối tiếp với R thay đổi .Khi R = 20 Ω thì công suất trên điện trở R cực đại và đồng thời khi đó điều chỉnh tụ C thì điện áp hiệu dụng hai đầu tụ C sẽ giảm . Dung kháng của tụ sẽ là :
A. 20 Ω B . 30 Ω C . 40 Ω D . 10 Ω
Giải :
Khi R thay đổi; công suất trên điện trở R cực đại khi R = | ZL - ZC | (1)
Đồng thời lúc này điều chỉnh tụ C thì điện áp hai hiệu dụng đầu tụ C giảm
Chúng tỏ khi R = 20 Ω = | ZL - ZC | => UCMAX
Áp dụng khi UCMAX => ZC = ( R2 + ZL2 ) / ZL (2) và đương nhiên ZC > ZL
Từ (1) => ZL = ZC – R (3) thay (3) vào (2) => ZC = 2R = 40 Ω
=> chọn C
b.Trắc nghiệm:
Câu 1: Cho mạch điện như hình vẽ: ![]()
L = \(\frac{\sqrt{3}}{\pi }\) H; R = 100Ω,tụ điện có điện dung thay đổi được , điện áp giữa hai đầu mạch là uAB = 200cos100πt (V).
Để uAM vàuNB lệch pha một góc , thì điện dung C của tụ điện phải có giá trị ?
A. \(\sqrt{3}\pi\) .10-4F B. \(\frac{\pi }{\sqrt{3}}\).10-4F C. \(\frac{\sqrt{3}}{\pi }\).10-4F D. \(\frac{2\pi }{\sqrt{3}}\).10-4F
Câu 2: Cho mạch điện xoay chiều RLC, đoạn MB chỉ chứa tụ điện C. uAB= U0.cos2πft (V). Cuộn dây thuần cảm có L = 3/5π(H), tụ điện C = 10-3/24π(F). HĐT tức thời uMB và uAB lệch pha nhau 900. Tần số f của dòng điện có giá trị là:
A.60Hz B.50Hz C.100Hz D.120Hz
Câu 3: Cho mạch điện xoay chiều như hình vẽ.
![]()
\(u_{AB}=140\sqrt{2}cos100\pi t(V);U_{AM}=140V,U_{MB}=140V\) Biểu thức điện áp uAM là
A. \(140\sqrt{2}cos(100\pi t-\pi /3)V\) B. \(140\sqrt{2}cos(100\pi t+\pi /2)V\)
C. \(140\sqrt{2}cos(100\pi t+\pi /3)V\) D.\(140cos(100\pi t+\pi /2)V\)
Câu 4: Đoạn mạch xoay chiều như hình vẽ: Cho uAB=\(200\sqrt{2}cos100\pi t(V);C=\frac{10^{-4}}{\pi }F,U_{AM}=200\sqrt{3}V\);
UAM sớm pha \(\frac{\pi }{2}\)rad so với uAB. Tính R
A, 50Ω B, 25\(\sqrt{3}\)Ω C,75Ω D, 100Ω
Câu 5. Cho mạch điện LRC nối tiếp theo thứ tự trên. Biết R là biến trở, cuộn dây thuần cảm có L = 4/π(H), tụ có điện dung C = 10-4/π(F). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều ổn định có biểu thức: u = U0.sin100πt (V). Để điện áp uRL lệch pha π/2 so với uRC thì R bằng bao nhiêu?
A. R = 300Ω. B. R = 100Ω. C. R = 100Ω. D. R = 200Ω.
Câu 6. Cho một mạch điện RLC nối tiếp. R thay đổi được, L = 0,8/π H, C = 10-3/(6π) F. Đặt vào hai đầu đoạn mạch một điện áp có biểu thức: u = U0.cos100πt. Để uRL lệch pha p/2 so với u thì phải có
A. R = 20Ω. B. R = 40Ω. C. R = 48Ω. D. R = 140Ω.
Câu 7. Cho một đoạn mạch RLC nối tiếp. Biết L = 1/π H và C = 25/π mF, điện áp xoay chiều đặt vào hai đầu mạch ổn định và có biểu thức u = U0cos100πt. Ghép thêm tụ C’ vào đoạn chứa tụ C. Để điện áp hai đầu đoạn mạch lệch pha π/2 so với điện áp giữa hai đầu bộ tụ thì phải ghép thế nào và giá trị của C’ bằng bao nhiêu?
A. ghép C’//C, C’ = 75/π μF. B. ghép C’ntC, C’ = 75/π μF.
C. ghép C’//C, C’ = 25 μF. D. ghép C’ntC, C’ = 100 μF.
BÀI TẬP ĐIỆN VUÔNG PHA
CÔNG THỨC VẾ PHẢI BẰNG =1 RÚT GỌN PHẦN DÒNG ĐIỆN XOAY CHIỀU
1 – Đoạn mạch chỉ có L ; uL vuông pha với i :
\((\frac{u_{L}}{U_{OL}})^{2}+(\frac{i}{I_{0}})^{2}=1\)
2 – Đoạn mạch chỉ có tụ C ; uCvuông pha với i:
\((\frac{u_{C}}{U_{OC}})^{2}+(\frac{i}{I_{0}})^{2}=1\)
3- Đoạn mạch có LC ; uLC vuông pha với i:
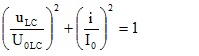
4 – Đoạn mạch có R và L ; uR vuông pha với uL
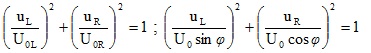
5 – Đoạn mạch có R và C ; uR vuông pha với uC
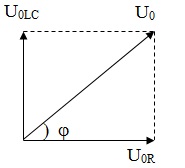
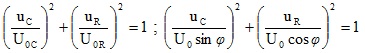
6 – Đoạn mạch có RLC ; uR vuông pha với uLC
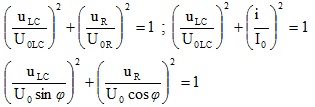
7 – Từ điều kiện để có hiện tượng cộng hưởng ω02LC = 1
Xét với ω thay đổi
7a : 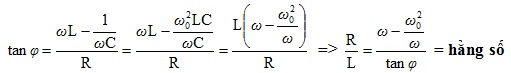
7b : ZL =ωL và \(Z_{C}=\frac{1}{\omega C}\)
![]()
=> đoạn mạch có tính cảm kháng ZL > ZC => ωL > ω0
=> đoạn mạch có tính dung kháng ZL < ZC => ωC < ω0
=> khi cộng hưởng ZL = ZC => ω =ω0
7c : I1 = I2 < Imax => ω1 ω 2 = ω 02 Nhân thêm hai vế LC
=> ω 1ω 2LC = ω 02LC = 1
=> ZL1 = ω1L và ZC2 = 1/ ω2C
=> ZL1 = ZC2 và ZL2 = ZC1
7d : Cosφ1 = cosφ2 => ω1ω 2LC = 1 thêm điều kiện L = CR2
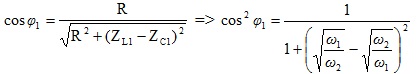
8 – Khi L thay đổi ; điện áp hai đầu cuộn cảm thuần L
ULmax <=> tanφRC. tanφRLC = – 1
9 – Khi C thay đổi ; điện áp hai đầu tụ C
UCmax <=> tanφRL. tanφRLC = – 1
10 – Điện áp cực đại ở hai đầu tụ điện C khi w thay đổi
\(\omega ^{2} ={\omega _{C}}^{2} = {\omega _{0}}^{2}-\frac{R^{2}}{2L^{2}};Z_{L}=\omega _{C}L\)và \(Z_{C}=1/\omega _{C}C\Rightarrow \frac{Z_{L}}{Z_{C}}={\omega _{C}}^{2}LC=\frac{{\omega _{C}}^{2}}{{\omega _{0}}^{2}}\)
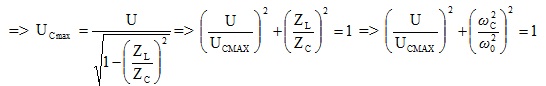
3.Xác định các đại lượng khi biết hai đoạn mạch có điện áp lệch pha góc j.
a. Các ví dụ:
Ví dụ 1: Một mạch điện không phân nhánh gồm điện trở thuần R = 75Ω, cuộn cảm có độ tự cảm L =\(\frac{5}{4\pi }H\) và tụ điện có điện dung C. Dòng điện xoay chiều qua mạch: i = 2 cos 100πt(A). Độ lệch pha giữa điện áp và cường độ dòng điện là π/4.Tính C.Viết biểu thức điện áp giữa hai đầu đoạn mạch trên.
Bài giải:
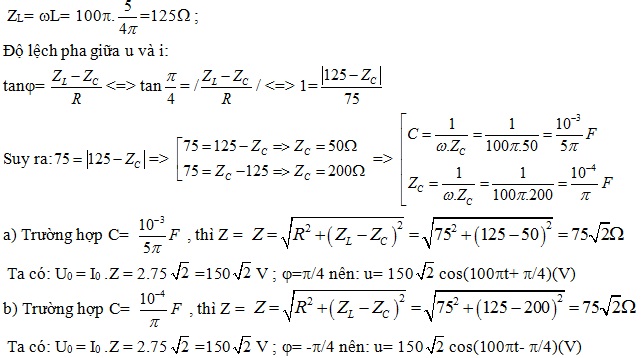
+ Ví dụ 2: Cho mạch xoay chiều như hình vẽ:
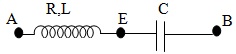
\(C=31,8(\mu F)\), f=50(Hz); Biết \(U_{AE}\) lệch pha \(U_{EB}\) một góc 1350 và i cùng pha với \(U_{AB}\). Tính giá trị của R?
A. R=50(Ω) B.R=50\(\sqrt{2}\)(Ω) C. R=100(Ω) D.R=200(Ω)
Bài giải: Theo giả thiết u và i cùng pha nên trong mạch xảy ra hiện tượng cộng hưởng ta có: \(Z_{L}=Z_{C}=\frac{1}{\omega C}=\frac{1}{100\pi .31,8.10^{-6}}=100(\Omega )\) . Mặt khác đoạn EB chứa tụ C nên \(\varphi _{EB}=\frac{-\pi }{2}=-90^{0}\)
Suy ra : \(\varphi _{AE}-\varphi _{EB}=135^{0}\) Hay :\(\varphi _{AE}=\varphi _{EB}+135^{0}=135^{0}-90^{0}=45^{0}\) ;
Vậy \(tan\varphi _{AE}=\frac{Z_{L}}{R}=tan45^{0}=1\rightarrow R=Z_{L}=100(\Omega )\).
Chọn C
b.Trắc nghiệm:
Câu 1: Đoạn mạch xoay chiều như hình vẽ
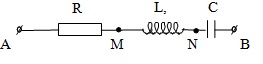
\(u_{AB}=100\sqrt{2}cos100\pi t(V),I=0,5A\)
\(u_{AN}\) sớm pha so với i một góc là \(\frac{\pi }{6}rad,u_{NB}\), trễ pha hơn uAB một góc \(\frac{\pi }{6}rad\).Tinh R
A, R=25Ω B, R=50Ω C, R=75Ω D,R=100Ω
Câu 2: Đoạn mạch xoay chiều như hình vẽ.\(u_{AB}=200cos100\pi t(V)\), I = 2A, \(u_{AN}=100\sqrt{2}(V)\)
\(u_{AN}\) lệch pha \(\frac{3\pi }{4}\)rad so với uMB Tính R, L, C
A,R=100Ω , L = \(\frac{1}{2\pi }H,C=\frac{10^{-4}}{\pi }F\) B,R=50Ω , L =\(\frac{1}{2\pi }H,C=\frac{10^{-4}}{2\pi }F\),
C, R=50Ω , L = \(\frac{1}{2\pi }H,C=\frac{10^{-4}}{\pi }F\) D, R=50Ω , L = \(\frac{1}{\pi }H,C=\frac{10^{-4}}{\pi }F\)
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Một số sơ đồ hay giải nhanh trắc nghiệm dao động điều hoà(10/04)
- Lý thuyết sóng cơ và sự truyền sóng cơ(31/05)
- Đại cương về dao động điều hòa ( có video)(09/04)
- Phương pháp giải bài tập sóng cơ và sự truyền sóng cơ(31/05)
- Bài tập trắc nghiệm dao động điều hòa có lời giải chi tiết(12/04)
- Bài tập lý thuyết về định nghĩa và các đại lượng đặc trưng của dao động cơ ( có đáp án)(08/04)
- Xác định các đại lượng đặc trưng của sóng(31/05)
- 300 Bài tập dao động cơ có đáp án(15/04)
- Bài tập trắc nghiệm lý thuyết: Vận tốc và gia tốc trong dao động điều hòa ( có đáp án)(08/04)
- Bài tập liên quan đến phương trình sóng(31/05)
chuyên đề được quan tâm
- Đại cương dòng điện xoay chiều
- Từ thông- Suất điện động cảm ứng xoay chiều
- Bài toán liên quan đến điện lượng
- Mạch điện xoay chiều RLC
- Độ lệch pha- giản đồ véctơ
- Hiện tượng cộng hưởng điện
- Phần quang học
- Đề kiểm tra giữa học kì 1 Vật Lí 10...
- Đề kiểm tra 45 phút - Vật Lí 12 -...
- Đề kiểm tra giữa học kì 1 - Vật Lí...
bài viết mới nhất
- Động năng - Định lý biến thiên động năng
- Trắc nghiệm Lực từ Lo - ren -xơ - Có...
- Hướng dẫn ôn tập học kỳ I - Vật lý...
- Bồi dưỡng học sinh giỏi: Áp suất. Áp suất chất...
- Bài tập nâng cao: Sự cân bằng lực - Lực...
- Đề thi chọn học sinh giỏi Vật Lí 9 -...
- Đề thi chọn học sinh giỏi lớp 9 - Năm...
- Công cơ học
- Đề thi chọn đội tuyển học sinh giỏi huyện môn...
- Đề thi chọn học sinh giỏi lớp 9 cấp THCS...
Cập nhật thông tin mới nhất của kỳ thi tốt nghiệp THPT 2025


