Giải nhanh trắc nghiệm vật lý 12 nhờ máy tính CASIO Fx-570ES & Fx-570ES plus, VINA CAL Fx-570ES plus

GIẢI NHANH TRẮC NGHIỆM VẬT LÝ 12 NHỜ MÁY TÍNH CASIO Fx-570ES & Fx-570ES Plus, VINACAL Fx-570ES Plus

PHẦN I: ỨNG DỤNG SỐ PHỨC TRONG BÀI TOÁN VẬT LÝ

- Dùng số phức trong bài toán viết phương trình dao động điều hòa

- Dùng số phức trong phép tổng hợp dao động điều hòa

- Dùng số phức trong các bài toán điện xoay chiều

I. KHÁI NIỆM VỀ SỐ PHỨC

1. Số phức \(\overline{x}\) là số có dạng \(\overline{x}\) = a + bi

Trong đó: a là phần thực: Re\(\overline{x}\) = a; b là phần ảo Im\(\overline{x}\) = b; i đơn vị ảo \(i^{2}=-1\)

2. Biểu diễn số phức \(\overline{x}\) = a+bi trên mặt phẳng phức: 

OM = r: mođun của số phức, \(r=\sqrt{a^{2}+b^{2}},\varphi :\) acgumen của số phức, \(tan\varphi =\frac{Im\overline{x}}{Re\overline{x}}\)

3. Dạng lượng giác của số phức:

Theo công thức Ole: \(\overline{x}=a+bi=r(cos\varphi +isin\varphi )=re^{i\varphi }=A\angle \varphi \left\{\begin{matrix}a=rcos\varphi \\ b=rsin\varphi \end{matrix}\right.\)

4. Biểu diễn một hàm điều hòa dưới dạng số phức:

Hàm điều hòa \(x=Acos\left ( \omega t+\varphi \right )\) biểu diễn vecto quay lại t = 0: 

\(x=Acos\left ( \omega t+\varphi \right )\leftrightarrow \overline{A}=\left\{\begin{matrix}\begin{vmatrix} \overline{A}=OM=A \end{vmatrix} \\ (Ox,\overrightarrow{OM})=\varphi \end{matrix}\right.\)

Ta thấy \(x=Acos\varphi ,b=Asin\varphi \rightarrow\) tại t = 0, biểu diễn x bởi: \(\overline{x}=a+bi=r(cos\varphi +isin\varphi )=re^{i\varphi }\)

 Vậy một hàm điều hòa (xét tại t = 0) có thể viết dưới dạng như sau:

\(x=Acos\left ( \omega t+\varphi \right )\)\(\Leftrightarrow \overline{x}=Ae^{i\varphi }=a+bi=A(cos\varphi +isin\varphi )=A\angle \varphi\)

với \(a=Acos\varphi , b=Asin\varphi ,\left\{\begin{matrix}A=a^{2}+b^{2} \\ tan\varphi =\frac{b}{a} \end{matrix}\right.\)

II. Viết phương trình dao động điều hòa

1. Cơ sở lý thuyết

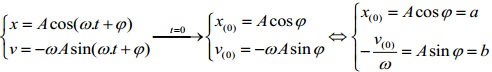
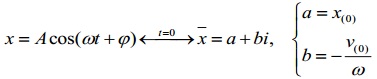
2. Phương pháp giải: Biết lúc t = 0 có:

\(\left\{\begin{matrix}a=x_{0} \\ b=-\frac{v_{0}}{\omega } \end{matrix}\right.\rightarrow \overline{x}=x_{0}-\frac{v_{0}}{\omega }i\rightarrow A\angle \varphi \rightarrow x=Acos\left ( \omega t+\varphi \right )\)

3. Chọn chế độ thực hiện tính số phức của máy: CASIO fx-570ES, 570ES plus, VINA CAL Fx-570ES plus

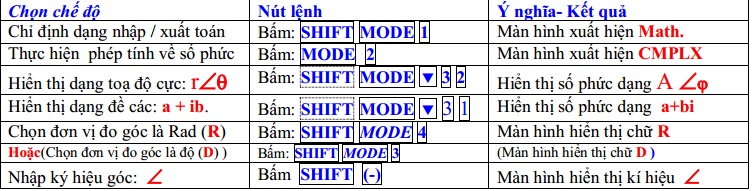
- Thao tác trên máy tính: Mode 2, và dùng đơn vị R (radian), bấm nhập: \(x_{0}=\frac{v_{0}}{\omega }i=\)

- Với máy fx 570ES, 570ES plus: muốn xuất hiện biên độ A và pha ban đầu \(\varphi\) làm như sau:

4. Ví dụ

Ví dụ 1: Vật m dao động điều hòa với tần số 0,5Hz, tại gốc thời gian nó có li độ \(x_{0}=4cm\), vận tốc \(v_{0}=12,56cm/s\) lấy \(\pi =3,14\). Hãy viết phương trình dao động

Giải: Tính \(\omega =2\pi f=2.\pi .0,5=\pi (rad/s)\)

\(t=0:\left\{\begin{matrix}a=x_{=4} \\ b=-\frac{v_{0}}{\omega }=-4 \end{matrix}\right.\rightarrow \overline{x}=4-4i\) 

Nhập 4 - 4i = SHIFT23 = 4\(\sqrt{2}\angle -\frac{\pi }{4}\rightarrow x=4\sqrt{2}cos(\pi t=\frac{\pi }{4})(cm)\)

Ví dụ 2: Một vật gắn vào đầu lò xo nhẹ. dao động điều hòa với chu kì 1s. Người ta kích thích bằng cách kéo m khỏi vị trí cân bằng ngược chiều dương một đoạn 3cm rồi buông. Chọn gốc tọa độ ở VTCB, gốc thời gian là lúc buông vật. Viết phương trình dao động

Giải: \(\omega =\frac{2\pi }{T}=2\pi (rad/s)\)

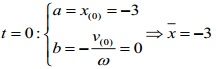
Nhập: -3 = SHIFT23 = \(3\angle \pi \Rightarrow x=3cos(2\pi t+\pi )(cm)\)