Cường độ điện trường do nhiều điện tích điểm gây ra ( cần thiết)
Cập nhật lúc: 12:35 18-08-2015 Mục tin: Vật lý lớp 11
Bài toán cường độ điện trường do nhiều điện tích điểm gây ra rất hay có trong các bài kiểm tra học kỳ. Bài viết giới thiệu phương pháp giải dạng bài tập này bạn đọc hãy tham khảo.
Xem thêm:
CƯỜNG ĐỘ ĐIỆN TRƯỜNG DO NHIỀU ĐIỆN TÍCH ĐIỂM GÂY RA
* Phương pháp:
- Xác định Véctơ cường độ điện trường: \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\)... của mỗi điện tích điểm gây ra tại điểm mà bài toán yêu cầu. (Đặc biệt chú ý tới phương, chiều)
- Điện trường tổng hợp: \(\overrightarrow{E}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}+...\)
- Dùng quy tắc hình bình hành để tìm cường độ điện trường tổng hợp ( phương, chiều và độ lớn) hoặc dùng phương pháp chiếu lên hệ trục toạ độ vuông góc Oxy
Xét trường hợp chỉ có hai Điện trường \(\overrightarrow{E}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}\)
a. Khí \(\overrightarrow{E_{1}}\) cùng hướng với \(\overrightarrow{E_{2}}\): \(\overrightarrow{E}\) cùng hướng với \(\overrightarrow{E_{1}},\overrightarrow{E_{2}}\):
E = E1 + E2
b. Khi \(\overrightarrow{E_{1}}\) ngược hướng với \(\overrightarrow{E_{2}}\): \(E=\begin{vmatrix} E_{1}-E_{2} \end{vmatrix}\)
\(\overrightarrow{E}\) cùng hướng với \(\left\{\begin{matrix}\overrightarrow{E_{1}} khi : E_{1}> E_{2} \\ \overrightarrow{E_{2}} khi : E_{1}< E_{2} \end{matrix}\right.\)
c. Khi \(\overrightarrow{E_{1}}\perp \overrightarrow{E_{2}}\): \(E=\sqrt{E_{1}^{2}+E_{2}^{2}}\)
\(\overrightarrow{E}\) hợp với \(\overrightarrow{E_{1}}\) một góc \(\alpha\) xác định bởi: \(tan\alpha =\frac{E_{2}}{E_{1}}\)
d. Khi E1 = E2 và tạo với nhau một góc \(\alpha\): \(E=2E_{1}cos\frac{\alpha }{2}\)
\(\overrightarrow{E}\) hợp với \(\overrightarrow{E_{1}}\) một góc \(\frac{\alpha }{2}\)
e.Trường hợp góc bất kì áp dụng định lý hàm cosin.
- Nếu đề bài đòi hỏi xác định lực điện trường tác dụng lên điện tích thì áp dụng công thức: \(\overrightarrow{F}=q\overrightarrow{E}\)
Bài 1: Cho hai điện tích q1 = 4.10-10C, q2 = -4.10-10C đặt ở A,B trong không khí, AB = a = 2cm. Xác định véc tơ cường độ điện trường tại:
a) H là trungđiểm của AB.
b) M cách A 1cm, cách B 3cm.
c) N hợp với A,B thành tam giác đều.
ĐS: a.72.103(V/m); b.32. 103(V/m); c.9000(V/m)
Bài 2: Hai điện tích q1 = 8.10-8C, q2 = -8.10-8C đặt tại A, B trong không khí, AB=4cm. Tìm véctơ cường độ điện trường tại C với:
a) CA = CB = 2cm.
b) CA = 8cm; CB = 4cm.
c) C trên trung trực AB, cách AB 2cm, suy ra lực tác dụng lên q = 2.10-9C đặt tại C.
ĐS: E song song với AB, hướng từ A tới B có độ lớn E = 12,7.105V/m; F = 25,4.10-4N)
Bài 3: Hai điện tích +q và – q (q >0) đặt tại hai điểm A và B với AB = 2a. M là một điểm nằm trên đường trung trực của AB cách AB một đoạn x.
a. Xác định vectơ cường độ điện trường tại M
b. Xác định x để cường độ điện trường tại M cực đại, tính giá trị đó
Hướng dẫn giải:
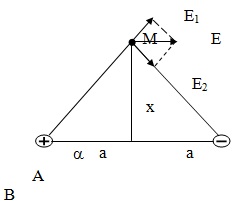
a. Cường độ điện trường tại M: \(\overrightarrow{E}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}\)
ta có: \(E_{1}=E_{2}=k\frac{q}{a^{2}+x^{2}}\)
Hình bình hành xác định là hình thoi: \(E=2E_{1}cos\alpha =\frac{2kqa}{(a+x)^{\frac{3}{2}}}(1)\)
b. Từ (1) Thấy để Emax thì x = 0: Emax = \(E_{1}=\frac{2kq}{a^{2}+x^{2}}\)
c) Lực căng dây: \(T=R=\frac{mg}{cos\alpha }=\sqrt{2}.10^{-2}N\)
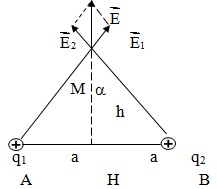
Bài 4 Hai điện tích q1 = q2 = q > 0 đặt tại A và B trong không khí. cho biết AB = 2a
a) Xác định cường độ điện trường tại điểm M trên đường trung trực của AB cách Ab một đoạn h.
b) Định h để EM cực đại. Tính giá trị cực đại này.
Hướng dẫn giải:
a) Cường độ điện trường tại M: \(\overrightarrow{E}=\overrightarrow{E_{1}}+\overrightarrow{E_{2}}\)
Ta có: \(E_{1}=E_{2}=k\frac{q}{a^{2}+x^{2}}\)
Hình bình hành xác định là hình thoi: \(E=2E_{1}cos\alpha =\frac{2kqa}{(a+x)^{\frac{3}{2}}}\)
b) Định h để EM đạt cực đại: \(a^{2}+h^{2}=\frac{a^{2}}{2}+\frac{a^{2}}{2}+h^{2}\geq 3.\sqrt[3]{\frac{a^{4}h^{2}}{4}}\)
\(\Rightarrow (a^{2}+h^{2})^{3}\geq \frac{27}{4}a^{4}h^{2}\Rightarrow (a^{2}+h^{2})^{\frac{3}{2}}\geq \frac{3\sqrt{3}}{2}a^{2}h\)
Do đó: \(E_{M}\leq \frac{2kqh}{\frac{3\sqrt{3}}{2}a^{2}h}=\frac{4kq}{3\sqrt{3}a^{2}}\)
EM đạt cực đại khi: \(h^{2}=\frac{a^{2}}{2}\Rightarrow h=\frac{a}{\sqrt{2}}\Rightarrow E_{M _{Max}}=\frac{4kq}{3\sqrt{3}a^{2}}\)
Bài 5 Tại 3 đỉnh ABC của tứ diện đều SABC cạnh a trong chân không có ba điện ích điểm q giống nhau (q<0). Xác định điện trường tại đỉnh S của tứ diện. (ĐS: \(\frac{kq\sqrt{6}}{a^{2}}\))
Bài 6 Hình lập phương ABCDA’B’C’D’ cạnh a trong chân không. Hai điện tích \(q_{1}=q_{2}=q> 0\) đặt ở A, C, hai điện tích \(q_{3}=q_{4}=-q\) đặt ở B’ và D’. Tính độ lớn cường độ điện trường tại tâm O của hình lập phương. (ĐS: \(\frac{16qk}{3\sqrt{3}a^{2}}\))
Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Trắc nghiệm Lực từ Lo - ren -xơ - Có đáp án (31/01)
- Tóm tắt lý thuyết chương cảm ứng điện từ(06/10)
- Đề kiểm tra giữa học kì 1 - Vật Lí 11 - THPT Phan Ngọc Hiển. Năm học 2016 - 2017. (Có đáp án và lời giải chi tiết)(03/10)
- Phân loại bài tập chương khúc xạ ánh sáng (24/03)
- Lý thuyết và bài tập chương khúc xạ ánh sáng - Có lời giải chi tiết.(16/03)
- Trắc nghiệm : Phản xạ toàn phần - Có đáp án(06/03)
- Phương pháp giải và các dạng bài tập chương từ trường(20/02)
- Các dạng bài tập chương cảm ứng điện từ(14/02)
- Đề thi học sinh giỏi sở GD&ĐT Vĩnh Phúc - Có lời giải chi tiết(10/02)
- Đề thi chọn HSG lớp 11 - Sở GD&ĐT Quảng Bình - Có lời giải chi tiết(17/01)
chuyên đề được quan tâm
- Đại cương dòng điện xoay chiều
- Từ thông- Suất điện động cảm ứng xoay chiều
- Bài toán liên quan đến điện lượng
- Mạch điện xoay chiều RLC
- Độ lệch pha- giản đồ véctơ
- Hiện tượng cộng hưởng điện
- Phần quang học
- Đề kiểm tra giữa học kì 1 Vật Lí 10...
- Đề kiểm tra 45 phút - Vật Lí 12 -...
- Đề kiểm tra giữa học kì 1 - Vật Lí...
bài viết mới nhất
- Động năng - Định lý biến thiên động năng
- Trắc nghiệm Lực từ Lo - ren -xơ - Có...
- Hướng dẫn ôn tập học kỳ I - Vật lý...
- Bồi dưỡng học sinh giỏi: Áp suất. Áp suất chất...
- Bài tập nâng cao: Sự cân bằng lực - Lực...
- Đề thi chọn học sinh giỏi Vật Lí 9 -...
- Đề thi chọn học sinh giỏi lớp 9 - Năm...
- Công cơ học
- Đề thi chọn đội tuyển học sinh giỏi huyện môn...
- Đề thi chọn học sinh giỏi lớp 9 cấp THCS...
Cập nhật thông tin mới nhất của kỳ thi tốt nghiệp THPT 2025


