Công thức tính nhanh động học chất điểm (chuẩn)

CÔNG THỨC TÍNH NHANH  ĐỘNG HỌC CHẤT ĐIỂM (CHUẨN)

I. Chuyển động thẳng đều:

    1. Vận tốc trung bình

    a.  Trường hợp tổng quát: \(v_{tb}=\frac{S}{t}\)

    b. Công thức khác: \(v_{tb}=\frac{v_{1}t_{1}+v_{2}t_{2}+...+v_{n}t_{n}}{t_{1}+t_{2}+...+t_{n}}\)

    c. Một số bài toán thường gặp:

Bài toán 1: Vật chuyển động trên một đoạn đường thẳng từ địa điểm A đến địa điểm B phải mất khoảng thời gian t. vận tốc của  vật trong nửa đầu của khoảng thời gian này là v₁ trong nửa cuối là  v₂. vận tốc trung bình  cả đoạn đường AB: \(v_{tb}=\frac{v_{1}+v_{2}}{2}\)

Bài toán 2: Một vật  chuyển động thẳng đều, đi một nửa quãng đường đầu với vận tốc v₁, nửa quãng đường còn lại với vận tốc v₂  Vận tốc trung  bình trên cả quãng đường: \(v=\frac{2v_{1}v_{2}}{v_{1}+v_{2}}\) 

    2. Phương trình chuyển động của chuyển động thẳng đều:     x = x₀ + v.t

3. Bài toán chuyển động của hai chất điểm trên cùng một phương:

    Xác định phương trình chuyển động của chất điểm 1:

x₁ = x₀₁ + v₁.t (1)

    Xác định phương trình chuyển động của chất điểm 2:

x₂ = x₀₂ + v₂.t (2)

    Lúc hai chất điểm gặp nhau x₁ = x₂  t thế t vào (1) hoặc (2) xác định được vị trí gặp nhau

     Khoảng cách giữa hai chất điểm tại thời điểm t: \(d=\begin{vmatrix} x_{01}-x_{02}+(v_{01}-v_{02})t \end{vmatrix}\)

II. Chuyển động thẳng biến đổi đều

1. Vận tốc:  v = v₀  + at

2. Quãng đường: \(s=v_{0}t+\frac{at^{2}}{2}\)

3. Hệ thức liên hệ: \(v^{2}-{v_{0}}^{2}=2as\rightarrow v=\sqrt{{v_{0}}^{2}+2as}=\frac{v^{2}-{v_{0}}^{2}}{2a}\)

4. Phương trình chuyển động: \(x=x_{0}+v_{0}t+\frac{at^{2}}{2}\)

Chú ý: Chuyển động thẳng nhanh dần đều a.v > 0.; Chuyển động thẳng chậm dần đều a.v < 0

5. Bài toán gặp nhau của chuyển động thẳng biến đổi đều:

    - Lập phương trình toạ độ của mỗi chuyển động : \(x_{1}=x_{01}+v_{01}t+\frac{a_{1}t^{2}}{2},x_{1}=x_{02}+v_{02}t+\frac{a_{2}t^{2}}{2}\)

    - Khi hai chuyển động gặp nhau: x₁ = x₂  Giải phương trình này để đưa ra các ẩn của bài toán.

     Khoảng cách giữa hai chất điểm tại thời điểm t: \(d=\begin{vmatrix} x_{1}-x_{2} \end{vmatrix}\)

6. Một số bài toán thường gặp:

Bài toán 1: Một vật chuyển động thẳng nhanh dần đều đi được những đoạn đường s₁và s₂  trong hai khoảng thời gian liên tiếp bằng nhau là  t. Xác định vận tốc đầu và gia tốc của vật.

    Giải hệ phương trình: 

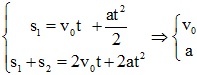
Bài toán 2: Một vật bắt đầu chuyển động thẳng nhanh dần đều. Sau khi đi được quãng đường s₁ thì vật đạt vận tốc v₁. Tính vận tốc của vật  khi đi được quãng đường s₂  kể từ khi vật bắt đầu chuyển động.

\(v_{2}=v_{1}\sqrt{\frac{s_{2}}{s_{1}}}\)

Bài toán 3:Một vật bắt đầu chuyển động nhanh dần đều không vận tốc đầu:

    - Cho gia tốc a thì quãng đường vật đi được trong giây thứ n: \(\Delta s=na-\frac{a}{2}\)

    - Cho quãng đường vật đi được trong giây thứ n thì gia tốc xác định bởi: \(a=\frac{\Delta s}{n-\frac{1}{2}}\)   

Bài toán 4: Một vật đang chuyển động với vận tốc v₀ thì chuyển động chầm dần đều:

    - Nếu cho gia tốc a thì quãng đường vật đi được cho đến khi dừng hẳn: \(s=\frac{-{v_{0}}^{2}}{2a}\)

    - Cho quãng đường vật đi được cho đến khi dừng hẳn s, thì gia tốc: \(a=\frac{-{v_{0}}^{2}}{2s}\)

    - Cho  a. thì thời gian chuyển động: t = \(\frac{-v_{0}}{a}\)

    - Nếu cho gia tốc a, quãng đường vật đi được trong giây cuối cùng: \(\Delta s=v_{0}+at-\frac{a}{2}\)

    - Nếu cho quãng đường vật đi được trong giây cuối cùng là \(\Delta s\), thì gia tốc : \(a=\frac{\Delta s}{t-\frac{1}{2}}\)

Bài toán 5: Một vật chuyển động thẳng biến đổi đều với gia tốc a, vận tốc ban đầu v₀:

    - Vận tốc trung bình của vật từ thời điểm t₁ đến thời điểm t₂: \(v_{tb}=v_{0}+\frac{\left ( t_{1}+t_{2} \right )a}{2}\)

    - Quãng đường vật đi được từ thời điểm t₁ đến thời điểm t₂: \(s=v_{0}(t_{2}-t_{1})+\frac{\left ( t_{2}^{2}-t_{1}^{2} \right )a}{2}\)

Bài toán 6:  Hai xe chuyển động thẳng đều trên cùng 1 đường thẳng với các vận tốc không đổi. Nếu đi ngược chiều nhau, sau thời gian t khoảng cách giữa 2 xe giảm một lượng a.  Nếu đi cùng chiều nhau, sau thời gian t khoảng cách giữa 2 xe giảm một lượng b. Tìm vận tốc mỗi xe.       

Giải hệ phương trình:

III. Sự rơi tự do: Chọn gốc tọa độ tại vị trí rơi, chiều dương hướng xuông, gốc thời gian lúc vật bắt đầu rơi.

    1. Vận tốc rơi tại thời điểm t: v = gt.

    2. Quãng đường đi được của vật sau thời gian t: \(s=\frac{1}{2}gt\)

    3. Công thức liên hệ:  v² = 2gs

    4. Phương trình chuyển động: \(y=\frac{1}{2}gt^{^{2}}\)

    4. Một số bài toán thường gặp:

Bài toán 1: Một vật rơi tự do từ độ cao h: 

    - Thời gian rơi xác định bởi: \(t=\sqrt{\frac{2h}{g}}\)

    - Vận tốc lúc chạm đất xác định bởi: \(v=\sqrt{2gh}\)

    - Quãng đường vật rơi trong giây cuối cùng: \(\Delta s=\sqrt{2gh}-\frac{g}{2}\)

Bài toán 2: Cho quãng đường vật rơi trong giây cuối cùng:

    -Thời gian rơi xác định bởi: \(t=\frac{\Delta s}{g}+\frac{1}{2}\)

    - Vận tốc lúc chạm đất: \(v=\Delta s+\frac{g}{2}\)

    - Độ cao từ đó vật rơi: \(h=\frac{g}{2}.\left ( \frac{\Delta s}{g} +\frac{1}{2}\right )^{2}\)

Bài toán 3: Một vật rơi tự do:

    - Vận tốc trung bình của chất điểm từ thời điểm t₁ đến thời điểm t₂: \(v_{tb}=\frac{(t_{1}+t_{2})g}{2}\)

    - Quãng đường vật rơi được từ thời điểm t₁ đến thời điểm t₂: \(s=\frac{(t_{2}^{2}-t_{1}^{2})g}{2}\)

IV. Chuyển động ném đứng  từ dưới lên từ mặt đất với vận tốc ban đầu v₀: Chọn chiểu dương thẳng đứng hướng lên, gốc thời gian lúc ném vật.

    1. Vận tốc: v = v₀ - gt

    2. Quãng đường: \(s=v_{0}t-\frac{gt^{2}}{2}\)

    3. Hệ thức liên hệ: \(v^{2}-v_{0}^{2}=-2gs\)

    4. Phương trình chuyển động: \(y=y_{0}t-\frac{gt^{2}}{2}\)

    5. Một số bài toán thường gặp:

Bài toán 1: Một vật được ném thẳng đứng lên cao từ mặt đất với vận tốc đầu v₀ :

    - Độ cao cực đại mà vật lên tới: \(h_{max}=\frac{v_{0}^{2}}{2g}\)

    - Thời gian chuyển động của vật: \(t=\frac{2v_{0}}{g}\)

Bài toán 2: Một vật được ném thẳng đứng lên cao từ mặt đất . Độ cao cực đại mà vật lên tới là h _max

    - Vận tốc ném: \(v_{0}=\sqrt{2gh_{max}}\)

    - Vận tốc của vật tại độ cao h₁: \(v=\pm \sqrt{v_{0}^{2}-2gh_{1}}\)

V. Chuyển động ném đứng  từ dưới lên từ  độ cao h₀  với vận tốc ban đầu v₀ :

    Chọn gốc tọa độ tại mặt đất chiểu dương thẳng đứng hướng lên, gốc thời gian lúc ném vật.

    1. Vận tốc: v = v₀ - gt

    2. Quãng đường: \(s=v_{0}t-\frac{gt^{2}}{2}\)

    3. Hệ thức liên hệ: \(v^{2}-v_{0}^{2}=-2gs\)

    4. Phương trình chuyển động: \(y=h_{0}+v_{0}t-\frac{gt^{2}}{2}\)

    5. Một số bài toán thường gặp:

Bài toán 1: Một vật ở độ cao h₀ được ném thẳng đứng lên cao với vận tốc đầu v₀ :

    - Độ cao cực đại mà vật lên tới: \(h_{max}=h_{0}+\frac{v_{0}^{2}}{2g}\)

    -  Độ lớn vận tốc lúc chạm đất: \(v=\sqrt{v_{0}^{2}+2gh_{0}}\)

    - Thời gian chuyển động: \(t=\frac{\sqrt{v_{0}^{2}+2gh_{0}}}{g}\)       

Bài toán 2: Một vật ở độ cao h₀ được ném thẳng đứng lên cao. Độ cao cực đại mà vật lên tới là h_max :

    - Vận tốc ném: \(v_{0}=\sqrt{2g(h_{max}-h_{0})}\)

    - Vận tốc của vật tại độ cao h₁: \(v=\pm \sqrt{v_{0}^{2}+2g(h_{0}-h_{1})}\)

    - Nếu bài toán chưa cho h₀ , cho  v₀ và h_max thì: \(h_{0}=h_{m_{ax}}-\frac{v_{0}^{2}}{2g}\) 

VI. Chuyển động ném đứng từ trên xuống : Chọn gốc tọa độ tại vị trí ném ; chiểu dương thẳng đứng hướng vuống, gốc thời gian lúc ném vật.

    1. Vận tốc: v = v₀ + gt

    2. Quãng đường: \(s=v_{0}t+\frac{gt}{2}\)

    3. Hệ thức liên hệ: \(v^{2}-v_{0}^{2}=2gs\)

    4. Phương trình chuyển động: \(y=y_{0}+\frac{gt^{2}}{2}\)

    5. Một số bài toán thường gặp:

Bài toán 1: Một vật ở độ cao h được ném thẳng đứng hướng xuống với vận tốc đầu v₀:

    - Vận tốc lúc chạm đất: \(v_{max}=\sqrt{v_{0}^{2}+2gh}\)

    - Thời gian chuyển động của vật: \(t=\frac{\sqrt{v_{0}^{2}+2gh-v_{0}}}{g}\)

    - Vận tốc của vật tại độ cao h₁: \(v=\sqrt{v_{0}^{2}+2g(h-h_{1})}\)